Microstructure Lectures

Table of Contents:

1. Introduction
2. Cracks: Atomistic - at Interfaces - in a Continuum
3. Cracks Near Interfaces Between Dissimilar Isotropic Materials
4. Introduction to Mechanical Behavior of Anisotropic Laminates
   • 4.1 Introduction to Mechanical Behavior of Anisotropic Materials
   • 4.2 Introduction to Mechanical Behavior of Laminates
5. Laminate Singularities Caused by Anisotropy: "Free-Edge Problem"
6. Laminate Singularities Caused by Ply Cracks
7. Cracks Near Interfaces Between Dissimilar Anisotropic Materials
   ------ Extension to a Homogeneous Continuum ------

8. Cracks in Homogeneous Isotropic Materials
9. Cracks in Homogeneous Anisotropic Materials
10. Wave Propagation in Homogeneous Isotropic/Anisotropic Materials
11. References

---

3.0 Cracks Near Interfaces Between Dissimilar Isotropic Materials

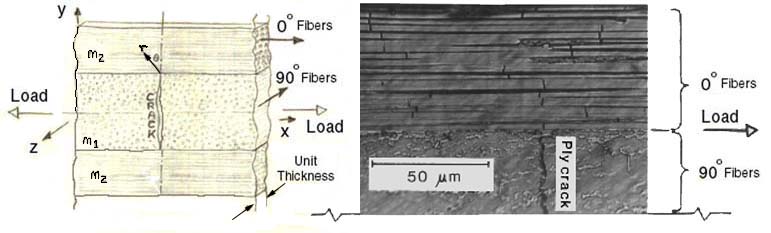
Numerous models for interfacial cracks exist. In the most general case we assume a crack arrested at an interface separating two dissimilar anisotropic materials and then simplify the model to dissimilar isotropic materials. Such cracks are common in fiber-reinforced composite laminates. In Figure 3 we show a schematic and an acetate replica micro-graph of a 90 degree ply crack arrested at a 0/90 degree ply interface.

Figure 3. Schematic and acetate replica micro-graph showing a ply crack arrested at a 0/90 ply interface

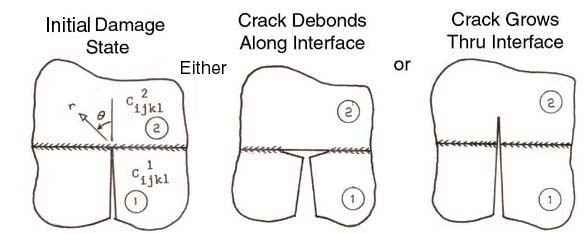
If the crack continues to propagate, it can grow into the adjacent 0^o ply, causing the fibers to fail or it can grow into an interfacial crack and debond along the 0/90 interface. Figure 4 shows experimental evidence of both types of crack growth, that can be controlled by the residual stress state, Ref.[1]. Statistical evidence confirms that laminate fracture strength is lower, if the ply crack extends into the 0^o load bearing ply, and higher if the ply crack extends along the interface as an interfacial debond. Hence we have experimental evidence that macroscopic laminate fracture strength is controlled by damage at the microscopic lamina scale.

With this experimental evidence the problem at hand is to create a model that will scale both the micro and macro and predict crack growth near an interface between two dissimilar materials. With such a model we can then study which parameters control crack growth. Does the residual stress state, anisotropy, or both control how the crack grows near an interface? The most general mathematical formulation is shown in Figure 5.

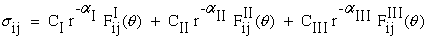(1)

From elementary fracture mechanics we can idealize the singular stresses near the ply crack tip as a linear superposition of Mode-I, Mode-II, Mode-III stress states. The superscripts and subscripts I, II, and III represent the three different fracture Modes. The exponent -α on the variable "r" (radius) has a value of -1/2 for isotropic and homogeneous anisotropic materials, but differs from -1/2 for dissimilar isotropic materials, which will be discussed below. The constants C_I, C_II, and C_III are functions of Stress Intensity and radius "r", and the variables F_ij^I, F_ij^II, and F_ij^III are functions of geometry only, i.e. location of boundaries and the angle, θ, measured at the crack tip. The remainder of this section will focus on deriving simple relationships for the special case of two dissimilar isotropic regions. After we learn more about anisotropy we will return to this problem where the dissimilar regions are anisotropic.

An introduction of the different fracture Modes is provided in classic fracture mechanics publications, Ref.[2,3] and at the Department of Materials Science and Engineering (MSE) Fracture Web Site (Student Team Project MSE2094, Spring 1997), see section on "Energy Methods " and "Stress Intensity"for an introduction to the different fracture Modes.

The first model of a crack near interfaces separating dissimilar isotropic materials was developed by Williams Ref.[4,5].

---

Interface Crack "Debond" Between Two Dissimilar Insotropic Materials

Williams Ref.[4] was the first to show that the singularity on "r" for an interfacial crack, "Debond" between two dissimilar materials, exhibited an oscillating singularity.

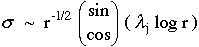(2)

Derivation of this equation will be outlined and discussed in class. Although the solution is correct mathematically, the strong oscillation predicted as the observer approaches the crack tip is physically unrealistic. Research by Dan Post, Professor at Virginia Tech, experimentally confirm a stress reversal near a debond crack by high resolution Moire Interferometry but although this is an encouraging piece of information it is far from what we need to confirm a full oscillation. Whether or not such a oscillating singularity can exist in a real material and at what scale such an oscillation might exist is exactly the type of question that arises when we try to interpret and justify model predictions. Although we are at the micro level were the crack behavior is controlled by two "thin" dissimilar isotropic materials we still assume a continuum but this approximation breaks down as we approach atomic spacing ("nano"). Are such oscillating singularities a realistic mechanical behavior that can be modeled at the nano scale? Probably not. At this point this type of behavior is at best only an interesting mathematical solution to a interfacial debond solution at the microscale that suggests that this behavior extends into the nanoscale -- maybe.

---

Crack Normal to Interface, "Ply Crack", Between Two Dissimilar Isotropic Materials

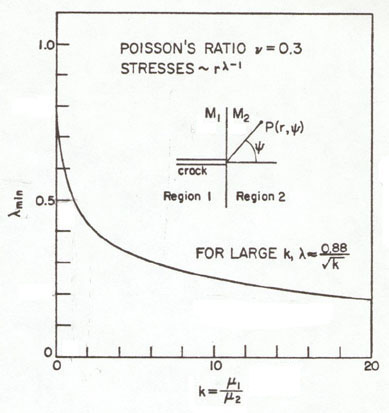
Williams Ref.[5] also showed that the singularity for a crack acting normal to an interface between two dissimilar isotropic regions is a function of the ratio of the elastic shear moduli of these two regions. Here we derive an expression for the exponent, λ on the radius "r". The exponent, λ is calculated as an eigenvalue or root from the characteristic equation below.

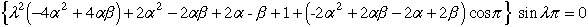(3)

Figure 6. Exponent singularity as a function of the ratio of shear moduli

DERIVATION OF EQUATIONS FOR PREDICTING THE STRESS SINGULARITY, λ

---